こんにちは、つくたろうです。

今回は、２リンク・３軸マニピュレータにおける逆運動学の式の導出について紹介します。

分野としては、ロボット工学やメカトロニクスの分野になると思いますが、数式の導出についての記事なので数学カテゴリに入れちゃいます（笑）

逆運動学とは
３軸・２リンクのマニピュレータの逆運動学の式の導出
おわりに

逆運動学とは

式の導出に先立って、「そもそも逆運動学とは何か」ということについて軽く説明したいと思います。

逆運動学というのは順運動学と対になる言葉・考え方です。

長さの分かっているリンクで構成されたマニピュレータについて、順運動学が「リンクの角度を与えた時にマニピュレータの手先位置の座標を得る」というものであることに対して、逆運動学は「マニピュレータの手先位置の座標を与えたときに、各リンクの角度を求める」というものになります。

例を紹介します。

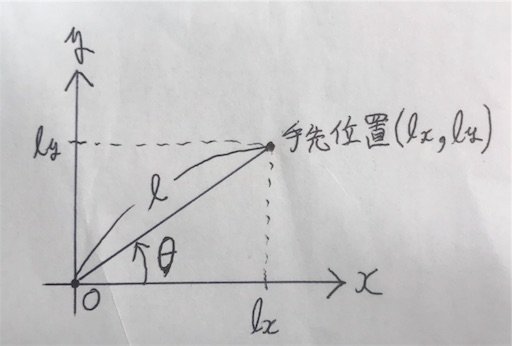
上図を、１リンク・１軸のマニピュレータの模式図だと思ってください。手描きですみません（笑）

原点に軸があって、マニピュレータの手先位置は $(l_x,l_y)$ とします。リンクの長さ $l$ 、回転角を $\theta$ とします。

このとき、簡単な三角関数を考えれば以下の式が成り立つことは皆さん分かると思います。
\begin{array} {}l_x = l \cos \theta \\ l_y = l \sin \theta \end{array}
ここで、 $l_x,l_y$ を $\theta$ の式で表現するのが順運動学、 $\theta$ を $l_x,l_y$ の式で表すのが逆運動学です。

この例については、上の三角関数の式から、
順運動学：
\begin{array} {}l_x = l \cos \theta \\ l_y = l \sin \theta \end{array}
逆運動学：
\begin{array} {} \displaystyle \theta = \arctan{ \left( \frac{l_y}{l_x} \right)} \end{array}
と、ともに簡単に求められると思いますが、軸やリンクが増えたときにも同じことができることが望ましいわけです。

３軸・２リンクのマニピュレータの逆運動学の式の導出

ということで、今から３軸・２リンクのマニピュレータの逆運動学について考えてみましょう。

ちなみに、３軸・２リンクの場合でも順運動学はそのまま簡単な三角関数として求められます。これについても導出の途中で紹介します。

問題設定

※数式が横に切れているときは、スライドすると先まで見ることができます。また、スマホを横向きにして見ると画面内に式全体が収まります。

今回は２リンク３軸マニピュレータの逆運動学の式の導出なので、以下のような模式図でマニピュレータを考えてみましょう。

３次元の座標系での模式図は上の通りで、図中の $\theta_0,\theta_1,\theta_2$ を、 $x,y,z$ の式で表します。

リンクの長さは図に示してある通り、 $l_1,l_2$ としています。

また、図二枚目の $S$ とは、 $S = \sqrt{x^{2} + z^{2}}$ を満たす、仮の座標軸です。計算をわかりやすくするために導入しています。

それでは、さっそく導出していきましょう！

逆運動学の式の導出

まず、先の模式図について三角関数での座標表記を考えることで、以下の式が得られます：
\begin{array}{} x = ( l_1 \cos{\theta_1} + l_2 \cos{\theta_2}) \cos{\theta_0} & \cdots (1) \\ y = l_1 \sin{\theta_1} + l_2 \sin{\theta_2} & \cdots (2)\\ z = ( l_1 \cos{\theta_1} + l_2 \cos{\theta_2}) \sin{\theta_0} & \cdots (3) \end{array}

これらの $(1),(2),(3)$ 式をまとめて式 $(A)$ とします。

この式 $(A)$ において、先ほど導入した $S = \sqrt{x^{2} + z^{2}}$ を満たす仮の座標 $S$ を用いると、上の $x,y,z$ を以下のように表すことができます：
\begin{array}{} y = l_1 \sin{\theta_1} + l_2 \sin{\theta_2} & \cdots{(1) ' }\\ S = l_1 \cos{\theta_1} + l_2 \cos{\theta_2} & \cdots{(2) '} \end{array}

これらの ${(1) '},{(2) '}$ 式をまとめて式 $(B)$ とします。

①： $\theta_0$ の導出

上記の式 $(A)$ のうち式 $(1),(3)$ において右辺同士、左辺同士でそれぞれ割ることで以下の式を得る：
\begin{array}{} \displaystyle \cfrac{z}{x} = \cfrac{\sin{\theta_0}}{\cos{\theta_0}} = \tan{\theta_0} \end{array}
したがって、 $\theta_0$ は、以下の通り。
\begin{array}{} \displaystyle \theta_0 = \arctan{\left( \cfrac{z}{x} \right)} & \cdots (a) \end{array}

メカトロニクス入門 (First Stageシリーズ)

実教出版

Amazon

②： $\theta_1$ の導出

上記の式 $(B)$ を変形して、
\begin{array}{} y - l_1 \sin{\theta_1} &=& l_2 \sin{\theta_2} \\ S - l_1 \cos{\theta_1} &= & l_2 \cos{\theta_2} \end{array}

両辺ともに2乗して足し合わせると、 $({l_2 \sin{\theta_2}})^{2} + ({l_2 \cos{\theta_2}})^{2} = {l_2}^{2}$ より以下の式を得る：
\begin{array}{} (y - l_1 \sin{\theta_1})^{2} + (S - l_1 \cos{\theta_1})^{2} &=& {l_2}^{2} \end{array}
これを展開して、
\begin{array}{} y^{2} - 2 y {l_1 \sin{\theta_1}} + {l_1 \sin{\theta_1}}^{2} + S^{2} - 2 S {l_1 \cos{\theta_1}} + {l_1 \cos{\theta_1}}^{2} &=& {l_2}^{2} \end{array} $({l_1 \sin{\theta_1}})^{2} + ({l_1 \cos{\theta_1}})^{2} = {l_1}^{2}$ を用いて整理すると、
\begin{array}{} y^{2} + S^{2} - 2 l_1 (y {\sin{\theta_1}} + S {\cos{\theta_1}}) &=& {l_2}^{2} - {l_1}^{2} \end{array}
よって、
\begin{array}{} \displaystyle \frac{y^{2} + S^{2} - ({l_2}^{2} - {l_1}^{2})}{2 l_1} &=& y {\sin{\theta_1}} + S {\cos{\theta_1}} \\ &=& \displaystyle \sqrt{y^{2} + S^{2}} \sin{(\theta_1 + \alpha)} & (\alpha = \arctan{\left( \cfrac{S}{y} \right)}、三角関数の合成) \end{array}
したがって、
\begin{array}{} \displaystyle \theta_1 + \alpha &=& \arcsin{ \left( \cfrac{y^{2} + S^{2} - ({l_2}^{2} - {l_1}^{2})}{2 l_1 \sqrt{y^{2} + S^{2}}}\right)} \end{array}
ここで、 $S^{2} = {x^{2} + z^{2}}$ および $\alpha = \arctan{\left( \cfrac{S}{y} \right)} = \arctan{\left( \cfrac{\sqrt{x^{2} + z^{2}}}{y}\right)}$ を代入すると、
\begin{array}{} \displaystyle \theta_1 + \arctan{\left( \cfrac{\sqrt{x^{2} + z^{2}}}{y}\right)} &=& \arcsin{ \left( \cfrac{x^{2} + y^{2} + z^{2} - ({l_2}^{2} - {l_1}^{2})}{2 l_1 \sqrt{x^{2} + y^{2} + z^{2}}}\right)} \end{array}
したがって、 $\theta_1$ は以下の通りとなる：
\begin{array}{} \displaystyle \theta_1 &=& \arcsin{ \left( \cfrac{x^{2} + y^{2} + z^{2} - ({l_2}^{2} - {l_1}^{2})}{2 l_1 \sqrt{x^{2} + y^{2} + z^{2}}}\right)} - \arctan{\left( \cfrac{\sqrt{x^{2} + z^{2}}}{y}\right)} & \cdots(b) \end{array}

③： $\theta_2$ の導出

$\theta_1$ と同様に式 $(B)$ を、今度は以下のように変形します：
\begin{array}{} y - l_2 \sin{\theta_2} &=& l_1 \sin{\theta_1} \\ S - l_2 \cos{\theta_2} &= & l_1 \cos{\theta_1} \end{array}

この変形は「 $\theta_1$ の時と、 $l$ と $\theta$ の添え字が入れ替わるだけ」であることが分かると思います。

したがって、あとは $\theta_1$ を求めるときと同じプロセスを行ってください。

答えも $l$ と $\theta$ の添え字が入れ替わるだけなので、 $\theta_2$ は以下のようになります：
\begin{array}{} \displaystyle \theta_2 &=& \arcsin{ \left( \cfrac{x^{2} + y^{2} + z^{2} - ({l_1}^{2} - {l_2}^{2})}{2 l_2 \sqrt{x^{2} + y^{2} + z^{2}}}\right)} - \arctan{\left( \cfrac{\sqrt{x^{2} + z^{2}}}{y}\right)} & \cdots(c) \end{array}

導出結果

上記の式 $(a)(b)(c)$ で求まったとおり、３軸・２リンクのマニピュレータの逆運動学の式（ ${\theta_0},{\theta_1},{\theta_2}$ を $x,y,z$ の式で表したもの）は、以下の通りになります：
\begin{array}{} \displaystyle \theta_0 &= \arctan{\left( \cfrac{z}{x} \right)} \\ \displaystyle \theta_1 &= \arcsin{ \left( \cfrac{x^{2} + y^{2} + z^{2} - ({l_2}^{2} - {l_1}^{2})}{2 l_1 \sqrt{x^{2} + y^{2} + z^{2}}}\right)} - \arctan{\left( \cfrac{\sqrt{x^{2} + z^{2}}}{y}\right)} \\ \displaystyle \theta_2 &= \arcsin{ \left( \cfrac{x^{2} + y^{2} + z^{2} - ({l_1}^{2} - {l_2}^{2})}{2 l_2 \sqrt{x^{2} + y^{2} + z^{2}}}\right)} - \arctan{\left( \cfrac{\sqrt{x^{2} + z^{2}}}{y}\right)} \end{array}